Contoh Persamaan Diferensial Stokastik



















Kesimpulan
Untuk eksperimen dan simulasi akan dicoba Persamaan Diferensial Stokastik menggunakan Stochastic Age-dependent Population (SAP) Equation (Wang, 2010) dan Cox-Ingersoll-Ross (CIR) Equation (Cox, 1985) yang terkenal dalam simulasi tingkat suku bunga
Stochastic Age-dependent Population Equation
Bentuk Stochastic Age-dependent Population Equation (Wang, 2010) sebagai berikut
(25)
(26)
(27)
(28)
dimana t∈(0,T), a∈(0,A), P(t,a) merupakan kepadatan populasi berumur a pada waktu t, B(t,a) merupakan tingkat kesuburan wanita berumur a pada saat t, u(t,a) merupakan tingkat kematian umur a pada saat
merupakan efek lingkungan ekternal populasi seperti emigrasi, gempa bumi, dll.
Beberapa asumsi untuk Stochastic Age-dependent Population Equation
-
(29) - (Lipschitz condition) terdapat sebuah konstanta positif k1 dan y1.y2 ∈Cy1, y2 ∈ C sedemikian sehingga

(30)
- (Linear growth) terdapat sebuaj konstanta positif k2 dan y ∈ C sedemikian sehingga
|f(t,y)| ⋁ ‖g(t,y ))‖2 ≤ k2|y|, a.e.t (31)
- μ(t), β(t) kontinu di Q sedemikian sehingga
0 ≤ μ ≤ μ(t) < ∞, 0 ≤ β(t) ≤ β< ∞ (32)
- gt(t, y(t)), gy(t, y(t)), gyy(t, y(t)) terbatas, dengan perkataan lain terdapat sebuaj konstanta N sedemikian sehingga
gt(t, y(t)) ∨ gy(t, y(t)) ∨ gyy(t, y(t)) ≤ N (33)
Cox – Ingersoll – Ross
CIR diperkenalkan pada tahun 1985 untuk memodelkan tingkat suku bunga instan. Secara umum persamaan CIR ditulis
dYt=k(θ-Yt) dt+ σYtdWt (34)
dimana σ merupakan sebuah difusi (proses Markov).
Experimen
Stochastic Age-dependent Population Equation
Sesuai dengan asumsi (29) – (33), simulasi dilakukan dengan menggunakan parameter - parameter (t) = β(t) = 1(1-t)2 , f(t, y) = -ty, g(t, y) = y, y0= e-1 , T = 1 dan Δt = 0.005.
Sehingga bentuk PDS (21) menjadi
dy=-t y dt+y dW (35)
y(0)=e-1 (36)
Dan mempunyai solusi eksplisit
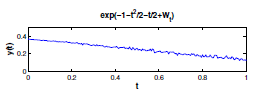
y(t) =exp(-1 - t22- t2 + Wt) (37)
Gambar 5. Solusi persamaan (30) - (31)
Pemilihan parameter dilakukan agar persamaan (21) menjadi PDS Geometric Brownian Motion
dYt=μ Yt dt+σ Yt dWt (38)
dimana persamaan (38) terkenal sudah mempunyai solusi eksplisit.
Wang melakukan perbandingan numerik antara Euler Maruyama eksplisit dengan Milstein eksplisit, Euler Maruyama semi implisit dengan Milstein semi implisit, dan Euler Maruyama implisit dengan Milstein implisit. Hasilnya Milstein lebih baik dibandingkan Euler Maruyama, hal ini sesuai dengan strong order Milstein yang lebih besar dibandingkan Euler Maruyama
Gambar 6. Simulasi pada paper Wang
Kemudian dilakukan simulasi ulang dengan menggunakan metode Euler Maruyama (19)-(20) dan Milstein (22)-(23), didapatkan nilai error seperti tertera pada tabel 1.
dt
|
EM eks.
|
Milstein Eks.
|
EM Semi Implicit
|
Milstein Semi Implicit
|
0.1
|
0.0233611
|
0.0033865
|
0.0195953
|
0.0025185
|
0.001
|
0.0194829
|
0.0017948
|
0.0196012
|
0.0017301
|
0.0001
|
0.0046903
|
0.0001851
|
0.0048619
|
0.0000117
|
Tabel 1. EM dan Milstein untuk eksplisit dan semi implicit
Sedangkan untuk metode implicit (21) dan (24) dilakukan percobaan dengan menambahkan parameter 𝛼 = 0.5 dan 𝛼 = 1 sehingga skema iterasinya menjadi
Xn+1= Xn+f(Xn+1)∆t+(1-α) g(Xn)∆Wn+αg(Xn+1)∆Wn (39)
Xn+1= Xn+f(Xn+1)∆t+(1-α) (g(Xn)∆Wn+12g(Xn)g'(Xn)(∆Wn2-∆t))+
α(g(Xn+1)∆Wn+12g(Xn+1)g'(Xn+1)(∆Wn2-∆t)) (40)
dan didapatkan nilai error seperti yang tertera pada tabel 2.
dt
|
EM Implicit
|
Milstein Implicit
| ||
𝛼 = 0.5
|
𝛼 = 1
|
𝛼 = 0.5
|
𝛼 = 1
| |
0.1
|
0.0170550
|
0.0634479
|
0.0348084
|
0.0711060
|
0.001
|
0.1823054
|
0.5217672
|
0.2068324
|
0.5610204
|
0.0001
|
0.1960423
|
0.5061324
|
0.1878555
|
0.4935079
|
Tabel 2. EM dan Milstein implicit
Dari tabel 1 dapat disimpulkan Milstein memang lebih baik daripada EM, tatapi pada tabel 2 tidak bisa dikatakan demikian. Hal lain yang dapat disimpulkan adalah pemilihan step size dt mempengaruhi nilai error pada metode eksplisit, semi implisit dan implisit.
Kemudian dilakukan percobaan lagi untuk memecah skema semi implicit (16) dan (18) menggunakan parameter α∈[0,1] dan β∈[0,1]
Xn+1= Xn+(1-α)f(Xn)∆t+αf(Xn+1)∆t+(1-β) g(Xn)∆Wn+βg(Xn+1)∆Wn (41)
Xn+1= Xn+(1-α)f(Xn)∆t+αf(Xn+1)∆t+ (1-β) (g(Xn)∆Wn+12g(Xn)g'(Xn) (∆Wn2-∆t))+ β(g(Xn+1)∆Wn+12g(Xn+1)g'(Xn+1)(∆Wn2-∆t)) (42)
Simulasi menggunakan 3 stepsize yang berbeda, yaitu ∆t=110,1100,11000 . Hasil simulasi bisa dilihat pada tabel 3 – 8.
Untuk metode Milstein Implisit, saat menggunakan ∆t=110 (tabel 6) terdapat lonjakan error ketika menggunakan parameter β>0.5.
Berikut merupakan tabel dan grafik hasil error menggunakan PDS CIR.
b
| ||||||||||||
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
1
| ||
a
|
0
|
0.0088519
|
0.0107765
|
0.0154344
|
0.0238095
|
0.0375197
|
0.0593081
|
0.0940811
|
0.1513358
|
0.2517848
|
0.4511923
|
1.5545268
|
0.1
|
0.0082020
|
0.0099028
|
0.0142125
|
0.0220620
|
0.0349790
|
0.0555473
|
0.0883719
|
0.1423247
|
0.2366259
|
0.4224193
|
1.1564303
| |
0.2
|
0.0076023
|
0.0090917
|
0.0130723
|
0.0204252
|
0.0325936
|
0.0520129
|
0.0830084
|
0.1338751
|
0.2224683
|
0.3957688
|
0.9764347
| |
0.3
|
0.0070500
|
0.0083397
|
0.0120091
|
0.0188925
|
0.0303542
|
0.0486908
|
0.0779679
|
0.1259477
|
0.2092350
|
0.3710519
|
0.8628474
| |
0.4
|
0.0065423
|
0.0076433
|
0.0110185
|
0.0174578
|
0.0282520
|
0.0455678
|
0.0732293
|
0.1185063
|
0.1968561
|
0.3480999
|
0.7786100
| |
0.5
|
0.0060768
|
0.0069995
|
0.0100962
|
0.0161156
|
0.0262788
|
0.0426316
|
0.0687732
|
0.1115176
|
0.1852680
|
0.3267620
|
0.7106625
| |
0.6
|
0.0056511
|
0.0064053
|
0.0092385
|
0.0148604
|
0.0244270
|
0.0398709
|
0.0645817
|
0.1049511
|
0.1744125
|
0.3069031
|
0.6532206
| |
0.7
|
0.0052630
|
0.0058579
|
0.0084417
|
0.0136872
|
0.0226896
|
0.0372750
|
0.0606381
|
0.0987786
|
0.1642368
|
0.2884015
|
0.6032759
| |
0.8
|
0.0049105
|
0.0053548
|
0.0077023
|
0.0125915
|
0.0210598
|
0.0348343
|
0.0569271
|
0.0929742
|
0.1546924
|
0.2711476
|
0.5590635
| |
0.9
|
0.0045916
|
0.0048935
|
0.0070173
|
0.0115689
|
0.0195316
|
0.0325393
|
0.0534342
|
0.0875139
|
0.1457349
|
0.2550425
|
0.5194481
| |
1
|
0.0043045
|
0.0044717
|
0.0063835
|
0.0106152
|
0.0180991
|
0.0303817
|
0.0501461
|
0.0823755
|
0.1373234
|
0.2399966
|
0.4836446
| |
Tabel 3. EM, dt =0.1

b
| ||||||||||||
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
1
| ||
a
|
0
|
0.0003262
|
0.0016318
|
0.0049609
|
0.0109461
|
0.0204034
|
0.0343878
|
0.0542705
|
0.0818416
|
0.1194525
|
0.1702110
|
0.2382558
|
0.1
|
0.0003198
|
0.0016074
|
0.0049088
|
0.0108536
|
0.0202529
|
0.0341559
|
0.0539255
|
0.0813409
|
0.1187383
|
0.1692050
|
0.2368513
| |
0.2
|
0.0003136
|
0.0015832
|
0.0048571
|
0.0107616
|
0.0201033
|
0.0339254
|
0.0535826
|
0.0808433
|
0.1180286
|
0.1682054
|
0.2354557
| |
0.3
|
0.0003076
|
0.0015593
|
0.0048059
|
0.0106703
|
0.0199547
|
0.0336963
|
0.0532419
|
0.0803487
|
0.1173232
|
0.1672121
|
0.2340691
| |
0.4
|
0.0003017
|
0.0015356
|
0.0047551
|
0.0105796
|
0.0198071
|
0.0334687
|
0.0529032
|
0.0798571
|
0.1166222
|
0.1662250
|
0.2326914
| |
0.5
|
0.0002960
|
0.0015122
|
0.0047047
|
0.0104896
|
0.0196604
|
0.0332425
|
0.0525666
|
0.0793686
|
0.1159256
|
0.1652441
|
0.2313226
| |
0.6
|
0.0002905
|
0.0014891
|
0.0046547
|
0.0104002
|
0.0195147
|
0.0330177
|
0.0522320
|
0.0788830
|
0.1152332
|
0.1642694
|
0.2299625
| |
0.7
|
0.0002851
|
0.0014662
|
0.0046051
|
0.0103114
|
0.0193699
|
0.0327943
|
0.0518995
|
0.0784004
|
0.1145452
|
0.1633007
|
0.2286111
| |
0.8
|
0.0002799
|
0.0014436
|
0.0045559
|
0.0102232
|
0.0192261
|
0.0325722
|
0.0515691
|
0.0779208
|
0.1138613
|
0.1623382
|
0.2272684
| |
0.9
|
0.0002749
|
0.0014212
|
0.0045071
|
0.0101357
|
0.0190832
|
0.0323516
|
0.0512407
|
0.0774441
|
0.1131817
|
0.1613816
|
0.2259342
| |
1
|
0.0002700
|
0.0013991
|
0.0044587
|
0.0100488
|
0.0189412
|
0.0321324
|
0.0509143
|
0.0769703
|
0.1125063
|
0.1604311
|
0.2246085
| |
Tabel 4. EM, dt =0.01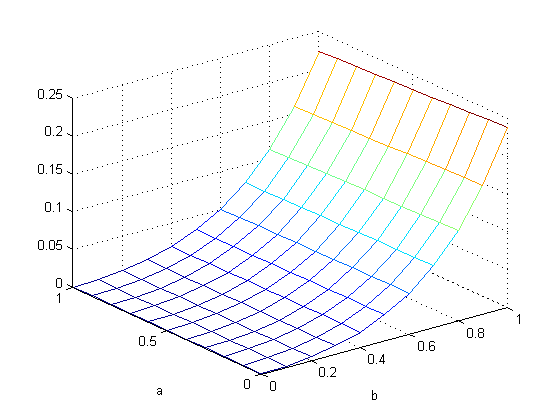
b
| ||||||||||||
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
1
| ||
a
|
0
|
0.0000379
|
0.0006885
|
0.0032901
|
0.0084831
|
0.0170775
|
0.0300963
|
0.0488283
|
0.0748951
|
0.1103344
|
0.1577048
|
0.2202167
|
0.1
|
0.0000381
|
0.0006873
|
0.0032867
|
0.0084762
|
0.0170656
|
0.0300773
|
0.0487992
|
0.0748521
|
0.1102724
|
0.1576172
|
0.2200946
| |
0.2
|
0.0000382
|
0.0006861
|
0.0032833
|
0.0084694
|
0.0170538
|
0.0300583
|
0.0487702
|
0.0748092
|
0.1102105
|
0.1575296
|
0.2199726
| |
0.3
|
0.0000383
|
0.0006848
|
0.0032798
|
0.0084625
|
0.0170420
|
0.0300393
|
0.0487411
|
0.0747662
|
0.1101486
|
0.1574420
|
0.2198507
| |
0.4
|
0.0000384
|
0.0006836
|
0.0032764
|
0.0084557
|
0.0170302
|
0.0300203
|
0.0487121
|
0.0747233
|
0.1100868
|
0.1573545
|
0.2197288
| |
0.5
|
0.0000385
|
0.0006824
|
0.0032729
|
0.0084489
|
0.0170183
|
0.0300014
|
0.0486831
|
0.0746805
|
0.1100249
|
0.1572671
|
0.2196070
| |
0.6
|
0.0000387
|
0.0006812
|
0.0032695
|
0.0084421
|
0.0170065
|
0.0299824
|
0.0486541
|
0.0746376
|
0.1099631
|
0.1571797
|
0.2194853
| |
0.7
|
0.0000388
|
0.0006799
|
0.0032661
|
0.0084353
|
0.0169947
|
0.0299635
|
0.0486252
|
0.0745948
|
0.1099014
|
0.1570924
|
0.2193636
| |
0.8
|
0.0000389
|
0.0006787
|
0.0032626
|
0.0084285
|
0.0169830
|
0.0299445
|
0.0485962
|
0.0745520
|
0.1098397
|
0.1570051
|
0.2192421
| |
0.9
|
0.0000390
|
0.0006775
|
0.0032592
|
0.0084217
|
0.0169712
|
0.0299256
|
0.0485673
|
0.0745092
|
0.1097780
|
0.1569179
|
0.2191205
| |
1
|
0.0000392
|
0.0006763
|
0.0032558
|
0.0084149
|
0.0169594
|
0.0299067
|
0.0485384
|
0.0744665
|
0.1097164
|
0.1568307
|
0.2189991
| |
Tabel 5. EM, dt =0.001
b
| ||||||||||||
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
1
| ||
a
|
0
|
0.0009137
|
0.0032182
|
0.0091299
|
0.0211307
|
0.0442264
|
0.0898877
|
0.1916051
|
3.0659583
|
2.5296281
|
4.3426107
|
78.6312135
|
0.1
|
0.0007374
|
0.0028244
|
0.0083610
|
0.0197065
|
0.0416027
|
0.0848598
|
0.1807332
|
542.9524042
|
2.2438494
|
3.9905775
|
57.1086401
| |
0.2
|
0.0005871
|
0.0024677
|
0.0076479
|
0.0183720
|
0.0391340
|
0.0801284
|
0.1705544
|
3.7522858
|
2.0065070
|
3.7024107
|
43.0581319
| |
0.3
|
0.0004613
|
0.0021458
|
0.0069876
|
0.0171222
|
0.0368110
|
0.0756743
|
0.1610167
|
1.1946015
|
1.8078421
|
3.4688953
|
33.4219121
| |
0.4
|
0.0003587
|
0.0018568
|
0.0063771
|
0.0159521
|
0.0346249
|
0.0714797
|
0.1520731
|
0.7321439
|
1.6407693
|
3.2833302
|
26.5503219
| |
0.5
|
0.0002778
|
0.0015989
|
0.0058136
|
0.0148572
|
0.0325677
|
0.0675282
|
0.1436804
|
0.5569796
|
1.5001570
|
3.1410627
|
21.4936475
| |
0.6
|
0.0002174
|
0.0013704
|
0.0052944
|
0.0138333
|
0.0306318
|
0.0638045
|
0.1357994
|
0.4643271
|
1.3823923
|
3.0392140
|
17.6753502
| |
0.7
|
0.0001764
|
0.0011696
|
0.0048171
|
0.0128764
|
0.0288102
|
0.0602946
|
0.1283942
|
0.4049856
|
1.2851590
|
2.9765647
|
14.7296512
| |
0.8
|
0.0001537
|
0.0009949
|
0.0043794
|
0.0119827
|
0.0270963
|
0.0569853
|
0.1214320
|
0.3621895
|
1.2074117
|
2.9535969
|
12.4156948
| |
0.9
|
0.0001482
|
0.0008450
|
0.0039792
|
0.0111489
|
0.0254840
|
0.0538646
|
0.1148825
|
0.3288736
|
1.1495986
|
2.9727145
|
10.5697769
| |
1
|
0.0001590
|
0.0007184
|
0.0036144
|
0.0103715
|
0.0239676
|
0.0509212
|
0.1087182
|
0.3015902
|
1.1142967
|
3.0387067
|
9.0775570
| |
Tabel 6. Milstein, dt =0.1
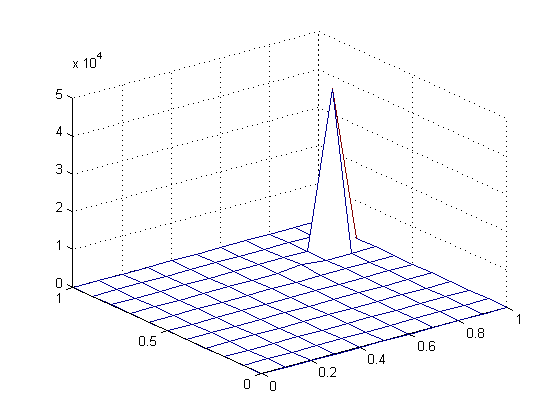
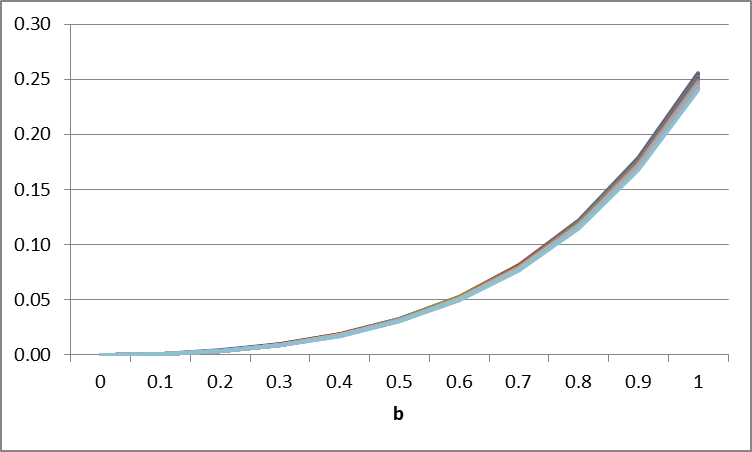
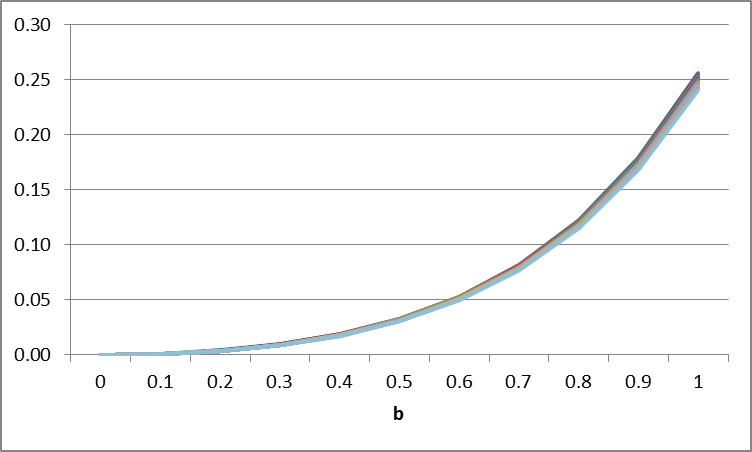
Pada gambar kiri bawah terdapat lonjakan error saat b = 0.7
Dilakukan 4 simulasi untuk Milstein dengan menggunakan dt = 0.1. Terlihat pada 4 gambar bahwa terjadi lonjakan error saat menggunakan parameter b > 0.5.
b
| ||||||||||||
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
1
| ||
a
|
0
|
0.0000046
|
0.0008853
|
0.0037593
|
0.0093129
|
0.0184530
|
0.0323852
|
0.0527209
|
0.0816305
|
0.1220615
|
0.1780551
|
0.2552156
|
0.1
|
0.0000036
|
0.0008680
|
0.0037162
|
0.0092309
|
0.0183143
|
0.0321646
|
0.0523840
|
0.0811292
|
0.1213287
|
0.1769967
|
0.2536978
| |
0.2
|
0.0000029
|
0.0008509
|
0.0036735
|
0.0091496
|
0.0181764
|
0.0319454
|
0.0520492
|
0.0806311
|
0.1206006
|
0.1759450
|
0.2521899
| |
0.3
|
0.0000022
|
0.0008341
|
0.0036312
|
0.0090689
|
0.0180395
|
0.0317277
|
0.0517164
|
0.0801360
|
0.1198770
|
0.1749000
|
0.2506919
| |
0.4
|
0.0000018
|
0.0008175
|
0.0035892
|
0.0089888
|
0.0179035
|
0.0315113
|
0.0513857
|
0.0796439
|
0.1191579
|
0.1738617
|
0.2492037
| |
0.5
|
0.0000014
|
0.0008011
|
0.0035476
|
0.0089092
|
0.0177683
|
0.0312962
|
0.0510571
|
0.0791550
|
0.1184434
|
0.1728299
|
0.2477252
| |
0.6
|
0.0000012
|
0.0007849
|
0.0035064
|
0.0088302
|
0.0176341
|
0.0310826
|
0.0507305
|
0.0786690
|
0.1177333
|
0.1718048
|
0.2462564
| |
0.7
|
0.0000012
|
0.0007690
|
0.0034655
|
0.0087519
|
0.0175008
|
0.0308703
|
0.0504060
|
0.0781861
|
0.1170276
|
0.1707862
|
0.2447971
| |
0.8
|
0.0000012
|
0.0007533
|
0.0034250
|
0.0086740
|
0.0173683
|
0.0306593
|
0.0500834
|
0.0777061
|
0.1163264
|
0.1697740
|
0.2433473
| |
0.9
|
0.0000015
|
0.0007379
|
0.0033849
|
0.0085968
|
0.0172368
|
0.0304496
|
0.0497629
|
0.0772291
|
0.1156295
|
0.1687683
|
0.2419070
| |
1
|
0.0000018
|
0.0007226
|
0.0033451
|
0.0085201
|
0.0171061
|
0.0302413
|
0.0494443
|
0.0767551
|
0.1149370
|
0.1677690
|
0.2404760
| |
Tabel 7. Milstein, dt =0.01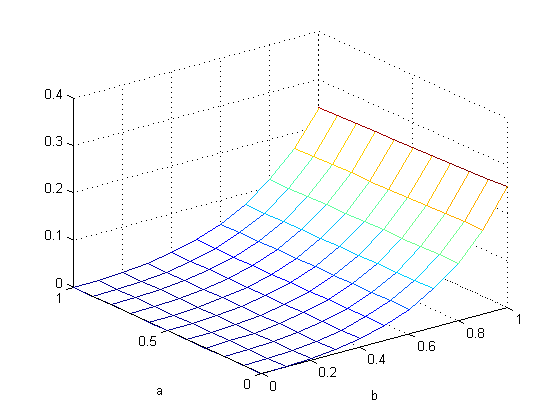
b
| ||||||||||||
0
|
0.1
|
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.7
|
0.8
|
0.9
|
1
| ||
a
|
0
|
0.0000046
|
0.0008853
|
0.0037593
|
0.0093129
|
0.0184530
|
0.0323852
|
0.0527209
|
0.0816305
|
0.1220615
|
0.1780551
|
0.2552156
|
0.1
|
0.0000036
|
0.0008680
|
0.0037162
|
0.0092309
|
0.0183143
|
0.0321646
|
0.0523840
|
0.0811292
|
0.1213287
|
0.1769967
|
0.2536978
| |
0.2
|
0.0000029
|
0.0008509
|
0.0036735
|
0.0091496
|
0.0181764
|
0.0319454
|
0.0520492
|
0.0806311
|
0.1206006
|
0.1759450
|
0.2521899
| |
0.3
|
0.0000022
|
0.0008341
|
0.0036312
|
0.0090689
|
0.0180395
|
0.0317277
|
0.0517164
|
0.0801360
|
0.1198770
|
0.1749000
|
0.2506919
| |
0.4
|
0.0000018
|
0.0008175
|
0.0035892
|
0.0089888
|
0.0179035
|
0.0315113
|
0.0513857
|
0.0796439
|
0.1191579
|
0.1738617
|
0.2492037
| |
0.5
|
0.0000014
|
0.0008011
|
0.0035476
|
0.0089092
|
0.0177683
|
0.0312962
|
0.0510571
|
0.0791550
|
0.1184434
|
0.1728299
|
0.2477252
| |
0.6
|
0.0000012
|
0.0007849
|
0.0035064
|
0.0088302
|
0.0176341
|
0.0310826
|
0.0507305
|
0.0786690
|
0.1177333
|
0.1718048
|
0.2462564
| |
0.7
|
0.0000012
|
0.0007690
|
0.0034655
|
0.0087519
|
0.0175008
|
0.0308703
|
0.0504060
|
0.0781861
|
0.1170276
|
0.1707862
|
0.2447971
| |
0.8
|
0.0000012
|
0.0007533
|
0.0034250
|
0.0086740
|
0.0173683
|
0.0306593
|
0.0500834
|
0.0777061
|
0.1163264
|
0.1697740
|
0.2433473
| |
0.9
|
0.0000015
|
0.0007379
|
0.0033849
|
0.0085968
|
0.0172368
|
0.0304496
|
0.0497629
|
0.0772291
|
0.1156295
|
0.1687683
|
0.2419070
| |
1
|
0.0000018
|
0.0007226
|
0.0033451
|
0.0085201
|
0.0171061
|
0.0302413
|
0.0494443
|
0.0767551
|
0.1149370
|
0.1677690
|
0.2404760
| |
Tabel 8. Milstein, dt =0.001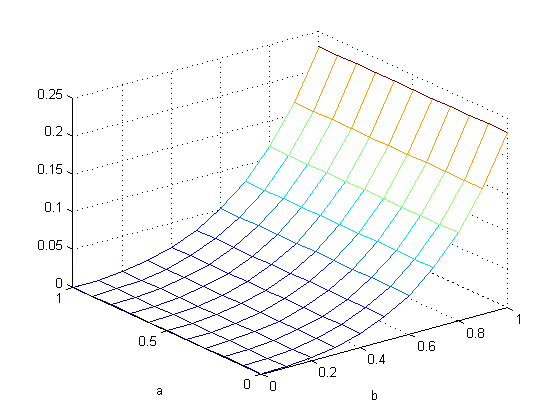
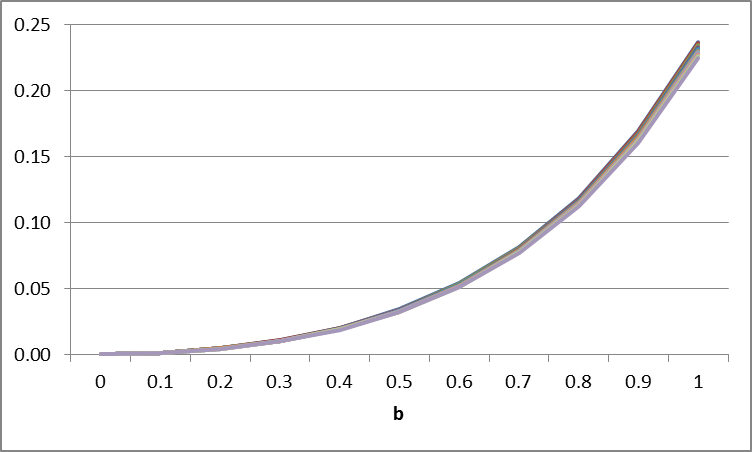
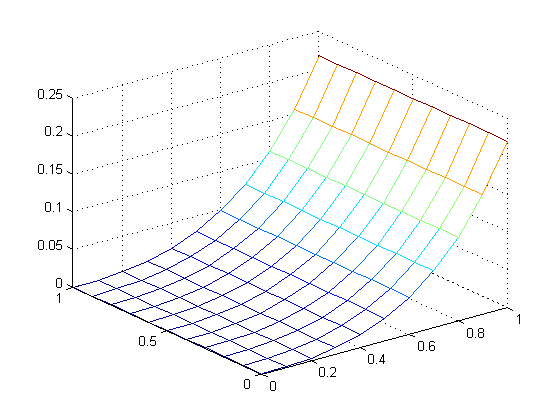
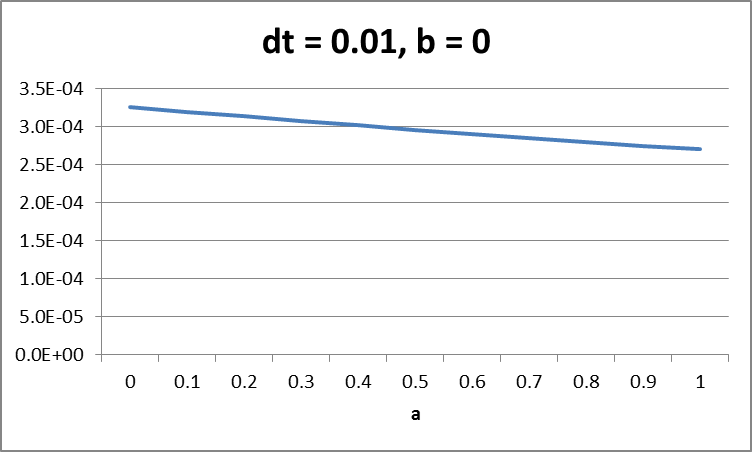
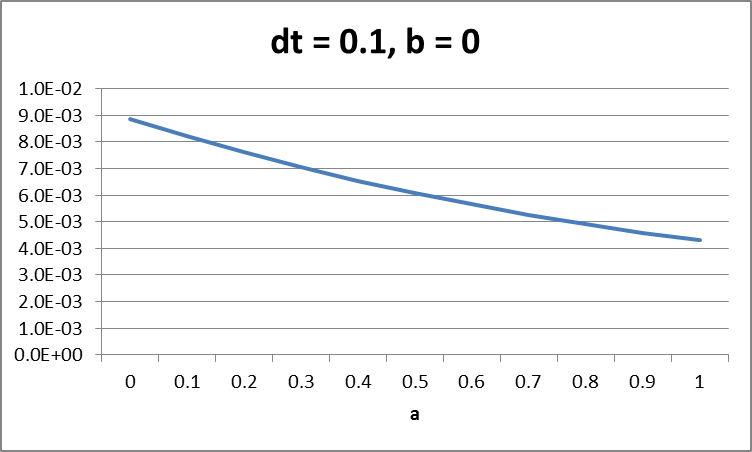
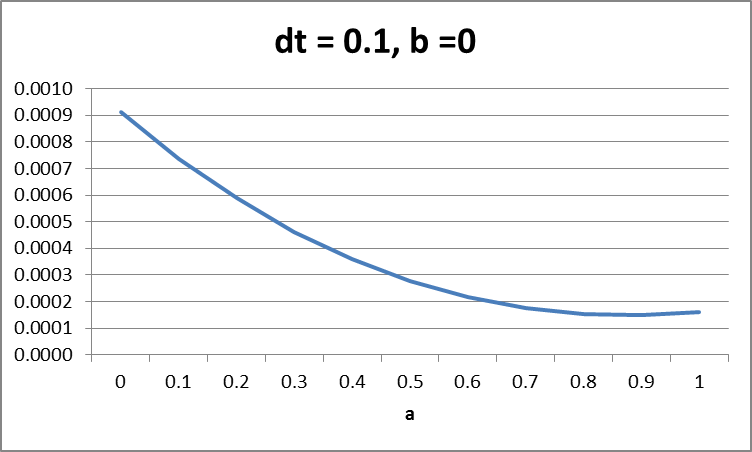
Dari tabel – tabel diatas dapat disimpulkan error terkecil berada pada kolom b = 0, sedangkan pada baris a bentuk grafiknya sebagai berikut,
EM dengan b=0 (semi implicit)
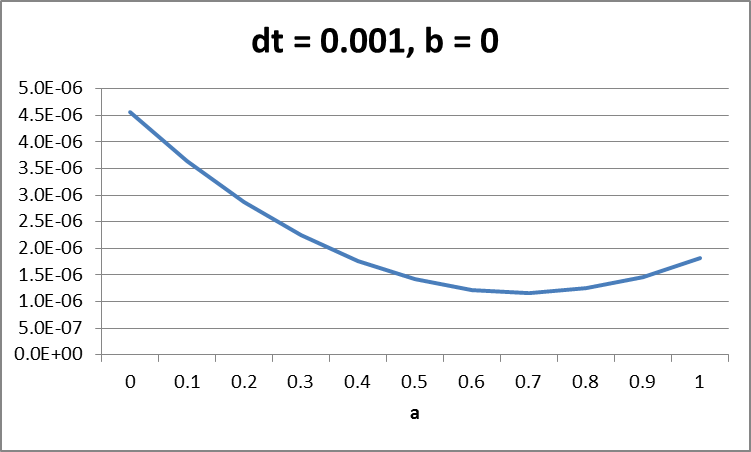
Milstein dengan b=0 (semi implicit)
Untuk metode EM sukar mengambil kesimpulan hubungan antara parameter a dan dt (stepsize). Sedangkan pada metode Milstein dapat dilihat semakin kecil step size maka error optimal (terkecil) akan mendekati nilai a = 0.
Cox – Ingersoll – Ross
Persamaan CIR dYt=k(θ-Yt) dt+ σYtdWt akan disimulasikan dengan parameter k=0.5, θ=0.2,σ=0.3, t∈[0,T] , T=1 , 10. Karena model CIR tidak mempunyai solusi explisit, maka akan digunakan step size yang lebih kecil dtshort=0.01 sebagai pengganti solusi explisit YT untuk mencari error dari metode numerik yang menggunakan step size yang panjang dtlong=0,1.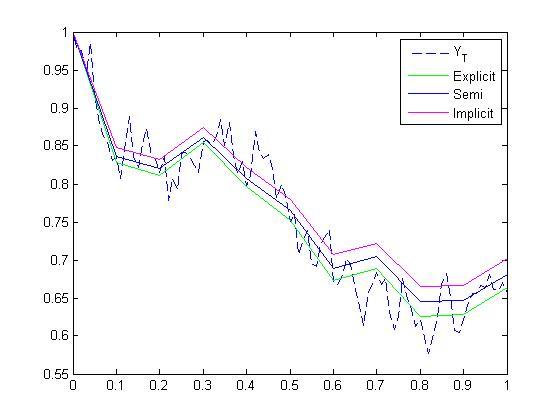
Explicit --> E(err)=0.0055
Semi Implicit --> E(err)=0.0109
Implicit --> E(err)=0.0558
Explicit --> E(err)=9.787x10-5
Semi Implicit --> E(err)=0.0375
Implicit --> E(err)=0.497
Metode eksplisit EM untuk CIR memberikan hasil yang paling baik (error terkecil) dibandingkan dengan metode semi implisit dan implisit EM. Hal ini mungkin karena untuk mendapatkan YT meskipun menggunakan step size yang kecil tetapi memakai metode eksplisit EM.
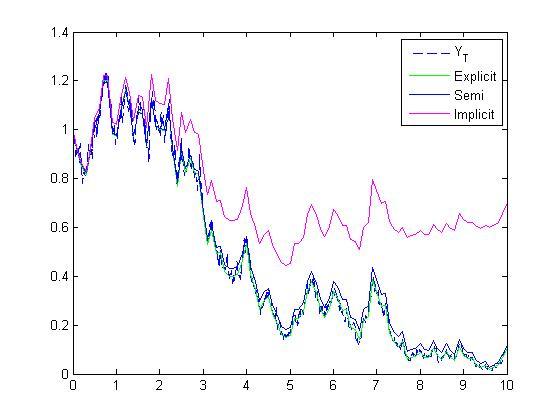
Sedangkan bila nilai T diperbesar (dalam hal ini T=10), bisa dilihat pada gambar jika metode implisit EM tidak stabil.
Explicit --> E(err)=0.00614
Semi Implicit --> E(err)=0.0104
Implicit --> E(err)=0.0549
Explicit --> E(err)=0.00106
Semi Implicit --> E(err)=0.0365
Implicit --> E(err)=0.4892
Sama seperti simulasi sebelumnya menggunakan EM, pada Milstein metode eksplisit lebih baik dibandingkan metode semi implisit dan implisit. Begitu juga ketika T diperbesar, bisa dilihat metode implisit Milstein tidak stabil.
T = 1
|
T = 10
| |||
EM
|
Milstein
|
EM
|
Milstein
| |
Explicit
|
0.0055
|
0.0061
|
9.79E-05
|
0.0011
|
Semi
|
0.0109
|
0.0104
|
0.0375
|
0.0365
|
Implicit
|
0.0558
|
0.0549
|
0.4969
|
0.4892
|
Metode Milstein dalam beberapa simulasi yang dilakukan lebih menunjukkan hasil yang baik dibandingkan dengan Euler Maruyama. Pemilihan step size mempengaruhi hasil dari metode eksplisit, semi implisit dan implisit. Sampai saat ini belum didapatkan teorema stepsize yang terbaik sehingga membuat salah satu metode eksplisit, semi implisit dan implisit hasilnya menjadi lebih baik diantara ketiganya.
Metode implisit dapat dikatakan yang terburuk diantara yang lain. Metode ini juga tidak stabil saat nilai T diperbesar (saat uji coba dengan persamaan CIR). Hal ini sepertinya yang menyebabkan sampai saat ini hanya ada integral Ito dan Stratonovich untuk menyelesaikan integral stokastik dimana masing-masing mengevaluasi titik kiri dan titik tengah.
Referensi
Carlsson, J. (2010). Stochastic Differential Equations: Models and Numerics.
Chockalingam, A., & Jayakumar, K. (2010). A Stochastic Control Approach To Avoiding Emergency Department Overcrowding. Proceedings of the 2010 Winter Simulation Conference. West Lafayette, USA: IEEE.
Cosimano, T., & Himonas, A. (2009). Mathematical Methods in Financial Economics.
Evans, L. C. (n.d.). An Introduction to Stochastic Differential Equations. Department of Mathematics UC Berkeley .
Hogan, M. (2008). Ito Integral and Stochastic Di.
Lord, G. J. (2010). Modified Semi{Implict Euler-Maruyama Scheme For Finite Element Discretization Of Spdes. Edinburgh: Department of Mathematics and Maxwell Institute, Heriot-Watt University.
Oksendal, B. (2000). Stochastic Differential Equations - An Introduction with Applications Fifth Edition. New York: Springer-Verlag Heidelberg .
Qihai, Z. (2009). Stochastic Differential Equations Numerical Simulation Algorithm for Financial Problems Based on Euler Method. 2009 International Forum on Information Technology and Applications. Chengdu: IEEE.
Spigler, R. (n.d.). Convergence analysis of the semi-implicit Euler method for abstract evolution equations. Minneapolis: Institute for Mathematics and its Applications, University of Minnesota.
Szatzschneider, W. (n.d.). Cox-Ingersoll-Ross (CIR) interest rate model.
Wang, H. (2010). Convergence Of Explicit Numerical Methods To Stochastic Age-dependent Population Equation. International Conference on Artificial Intelligence and Computational Intelligence. YinChuan: IEEE.
Wang, H. (2010). Numerical Methods To Stochastic Age-dependent Population Equations. 2010 International Conference on Artificial Intelligence and Computational Intelligence.
XIAO, Y. (2011). Convergence And Stability Of The Semi-Implicit Euler Method With Variable Stepsize For A Linear Stochastic Pantograph Differential Equation. INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING.









Komentar
Posting Komentar